
Contact Info
Australian National University
christoph.federrath@anu.edu.au
+61 (0)2 6125 0217
0000-0002-0706-2306
GitHub Bitbucket
The density variance-Mach number relation of the turbulent interstellar medium is relevant for theoretical models of the star formation rate, efficiency, and the initial mass function of stars. Here we use high-resolution hydrodynamical simulations with grid resolutions of up to 1024^3 cells to model compressible turbulence in a regime similar to the observed interstellar medium. We use FYRIS ALPHA, a shock-capturing code employing a high-order Godunov scheme to track large density variations induced by shocks. We investigate the robustness of the standard relation between the logarithmic density variance (sigma_s^2) and the sonic Mach number of isothermal interstellar turbulence, in the non-isothermal regime. Specifically, we test ideal gases with diatomic molecular (gamma = 7/5) and monatomic (gamma = 5/3) adiabatic indices. A periodic cube of gas is stirred with purely solenoidal forcing at low wavenumbers, leading to a fully developed turbulent medium. We find that as the gas heats in adiabatic compressions, it evolves along the relationship in the density variance-Mach number plane, but deviates significantly from the standard expression for isothermal gases. Our main result is a new density variance-Mach number relation that takes the adiabatic index into account: sigma_s^2 = ln(1+b^2*Mach^{(5*gamma+1)/3}) and provides good fits for b*Mach <= 1. A theoretical model based on the Rankine-Hugoniot shock jump conditions is derived, sigma_s^2 = ln{1+(gamma+1)*b^2*Mach^2/[(gamma-1)*b^2*Mach^2+2]}, and provides good fits also for b*Mach > 1. We conclude that this new relation for adiabatic turbulence may introduce important corrections to the standard relation, if the gas is not isothermal.
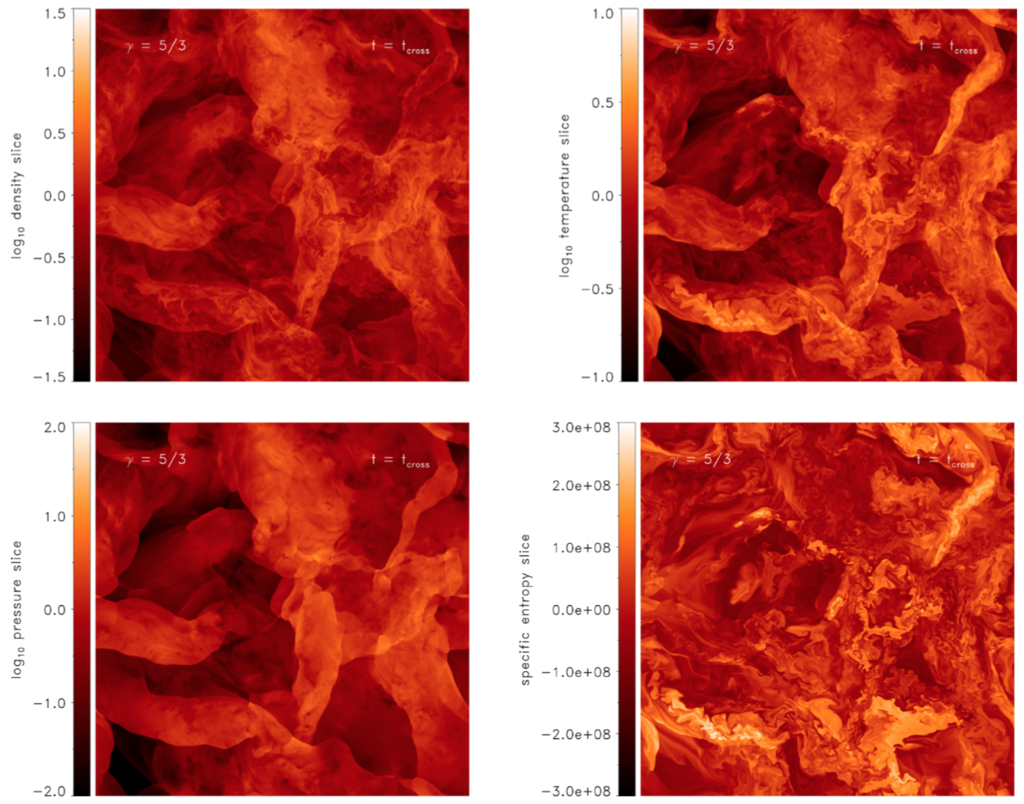
Slices of the normalized density (top left), temperature (top right), pressure (bottom left), and specific entropy (bottom right) in the non-isothermal turbulence simulations with adiabatic index gamma = 5/3. We see that gas at a given density can have a wide range of temperatures and pressures, unlike in a polytropic gas where the temperature and pressure are unique functions of the density only.
We thank the referee, Sam Falle, for his timely and constructive report, which improved the paper significantly. CF acknowledges funding provided by the Australian Research Council's Discovery Projects (grants DP130102078 and DP150104329). We gratefully acknowledge the Jülich Supercomputing Centre (grant hhd20), the Leibniz Rechenzentrum and the Gauss Centre for Supercomputing (grant pr32lo), the Partnership for Advanced Computing in Europe (PRACE grant pr89mu), and the National Computational Infrastructure (grants n72 and ek9), supported by the Australian Government. This work was further supported by resources provided by the Pawsey Supercomputing Centre with funding from the Australian Government and the Government of Western Australia.