Table of Contents
PyWiFeS Data Reduction
The processes in version 2 of PyWiFeS largely build upon the excellent work of the previous PyWiFeS developers. Thus, we retain the original documentation here, but note that several aspects have undergone significant revision in the current version, described in Onken et al. (in prep). Documentation for the new processes may also be found in our ReadTheDocs site or in the README and CHANGELOG files in the GitHub repository
This page details the algorithms and techniques employed in PyWiFeS data reduction procedures. For details on how to actually run the reduction script, see the main documentation page. For the ordered list of reduction steps in the default reduction script, see the default reduction steps page.
Image Pre-Processing
Overscan Subtraction
The very first step in WiFeS data reduction is to subtract the overscan level from the raw data. Regions of the raw data corresponding to the overscan regions and science data regions are handled automatically for all detector generations and epochs.
Bias subtraction
After subtraction of the (flat) overscan level, the detector bias level has some residual structure to it. This can be fitted from bias frames (see Figure below) and subtracted from science data. The bias level was been seen to drift by up to a few e- during a night for the 1st generation detectors.
Bad Pixel Cleanup
The 2nd generation detectors for WiFeS, installed in 2013, have a few dead columns in the CCDs (1 in blue, 2 in red, out of 4000+ columns). These are interpolated over as shown in the Figure below (top: before, bottom: after) and flagged in the data quality extensions of the MEF files.
Conversion to Multi-Extension Fits (MEF)
After initial pre-processing, WiFeS data is processed on a slitlet-by-slitlet basis. To better accommodate this, data from each slitlet is isolated and stored as a separate FITS extension in a multi-extention FITS (MEF) file format. The location of each slitlet is fitted from a flat lamp exposure by fitting the centre of each slitlet's profile (see Figure below).
The WiFeS MEF format has 25 extensions for the slitlet data, 25 extensions for the variance images, and 25 extensions for data quality flags. Currently the data quality flags are only used to flag pixels interpolated over in the bad pixel repair step or the cosmic ray rejection step, but may be made more complex in future iterations of the pipeline.
Cosmic Ray Rejection
Cosmic rays in WiFeS data are corrected using a highly modified version of the LA Cosmic algorithm developed by Pieter van Dokkum. The main adjustment required for WiFeS data is needed in the step where a smoothed sky background is derived and then subtracted from the observed data. Due to the curved wavelength solution for WiFeS, the data must be resampled to a rectilinear grid, smoothed along the cross-dispersion axis, then resampled to the original wavelength sampling (see Figure below). This sky-subtracted data can then be run through the Laplacian kernel as usual in LA Cosmic. The code for WiFeS also iterates over the 25 slitlets and collects data in the MEF format.
Wavelength Solution
The WiFeS wavelength solution is derived in three steps:
- Find emission lines in arc lamp data
- Determine the true wavelengths of those found lines.
- Fit for the wavelength solution across the entire detector, using the WiFeS optical model.
1. Finding the Lines: The first step, finding emission lines, is performed by default using the 'mpfit' method (see paper for details). This fits emission lines as Gaussians in linear wavelength space. A faster but less robust technique, 'loggauss', fits the emission lines in logarithmic flux space, where a Gaussian is merely a quadratic polynomial fit. Because this 'loggauss' method operates in logarithmic space, it cannot use fluxes close to zero, and provides a less robust fit (see Figure below), but is far more rapid due to the speed of polynomial fitting in NumPy, so is suitable only for times when a wavelength solution must be derived rapidly.
2. Associating lines to true wavelengths: Once the emission lines have been found, they must be associated with a true reference wavelength for the emitting atomic species. This is done by first calculating a predicted wavelength for the line's physical position on the detector, based on a reference wavelength solution. This then must be adjusted to determine the offset between the observed wavelength solution and the reference one. This step is generally performed by running a cross-correlation of the observed spectrum for each detector row with a known reference spectrum (with correct wavelength calibration) to derive a coherent shift for all lines in a given row. Each line's guessed wavelength is adjusted for this 'xcorr' shift, and a reference wavelength can then only be associated with a found emission line if they are nearest neighbours to each other.
3. Optical Model Wavelength Solution: Armed with the arc lamp emission line locations and reference wavelengths, these values can be used to constrain the parametrised optical model of the instrument wavelength solution (Sharp & Nielsen). A schematic of the incidence angles for light from the different slitlets is shown below, and illustrates how the optical geometry affects the wavelength solutions realised for each slitlet on the detector.
The optical model fitting routine proceeds in a number of steps, constraining groups of model parameters together. The final 42-parameter model consistently provides high precision wavelength solutions (RMS ~ 0.05Å for the R=7000 gratings, see residual plot below) which also has the advantage of behaving smoothly at the slitlet boundaries (as opposed to edge effects common to polynomial wavelength solution techniques).
Wavelength Solution Stability: For science applications requiring the most precise wavelength solutions (e.g., kinematic studies), WiFeS users should be aware that the instrument wavelength solution can drift by 50-100 km/s during a given night (see Figure below). This is due to the temperature dependence of the grating's effective dispersion (i.e., the l/mm count). For applications requiring better precision than this, local arc frames taken during the night are recommended.
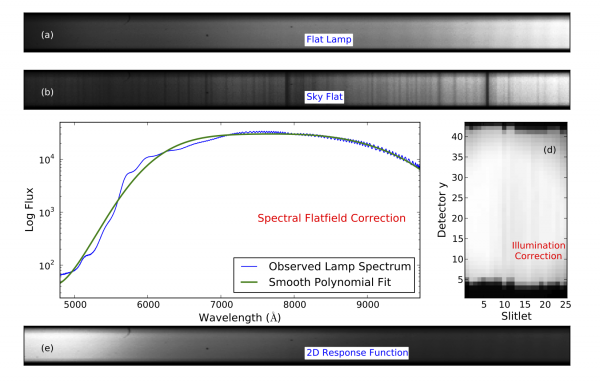
Flat-fielding
Flat-fielding for WiFeS is slightly complicated for two reasons: (1) the smooth spectrum quartz lamp in the WiFeS internal calibration unit does not provide uniform spatial illumination that mimics the illumination from the telescope; and (2) reflections internal to the WiFeS instrument create a diffuse glow and “horseshoe” reflection (see Figure below) which strongly affect the flatfield solution, especially at very blue wavelengths on the blue detector.
The internal reflections for WiFeS flat-field data are corrected using the novel 'interslice_cleanup' routine developed by Fred Vogt. This routine uses the space between slitlets to fit for the shape of the WiFeS internal reflections (see Figure below) and subtracts this reflection model from the flat-field data. This routine has provided excellent flat-fielding, and is especially important in yielding an accurate spatial flat-field (illumination) correction.
Ideally a flat-field solution should correct for three effects:
- Differences in quantum efficiency for individual pixels on the detector (i.e., “hot” or “cold” pixels).
- Rapid variations in the dichroic throughput with wavelength (dichroic “wiggles”) and its variation across the instrument field of view.
- Variation in the overall instrument throughput across the instrument field of view (i.e., spatial throughput, or “illumination”, variations).
For WiFeS, the first two are achieved with the smooth spectrum (quartz) lamp in the WiFeS calibration unit, while the final effect is corrected by use of twilight sky observations. A schematic representation of the PyWiFeS response function calculation is show below, and is described in greater detail in the PyWiFeS paper.
Data Cube Generation
Final WiFeS data cubes are generated by resampling the flux values at the observed (x,y,λ) positions onto a rectilinear grid grid of (α,δ,λ). The true y value for each pixel in the WiFeS field of view is derived using a wire frame observation (see Figure below).
Light from the same origin on the sky is dispersed to different positions due to the effect of Atmospheric Differential Refraction (ADR; Filippenko 1992), which is sometimes referred to as Differential Atmospheric Refraction (DAR). For WiFeS the ADR deflections in x and y are calculated (see Figure below) using observation details in the FITS header.
The true (α,δ) coordinates derived from the wire frame and ADR calculation, and the observed λ values from the wavelength solution, are used as input to the WiFeS cube generation routine. The output of this routine is still in MEF format (to facilitate visual inspection of individual slitlets).
Flux Calibration
After WiFeS data have undergone standard image processing steps (e.g., bias subtraction, cosmic ray rejection, flat-fielding), the absolute flux scale of the data must still be assessed. This is done by observing spectrophotometric standard stars and comparing their observed fluxes to reference spectra. In PyWiFeS this is done with the procedure outlined schematically in the Figure below, using routines defined in the 'wifes_calib' sub-module.
The flux calibration step corrects for the smooth instrument throughput curve, as well as atmospheric extinction. However sharp absorption features caused by molecules in the atmosphere (primarily O2 and H2O) remain, and must be corrected in object spectra (bottom panel below) by measuring their structure in the spectra of flux-calibrated smooth spectrum stars (top panel below).
Spectrophotometric Standard Star Catalogs
Flux calibration requires a set of reference spectra of spectrophotometric standard stars. Included in PyWiFeS are two spectra catalogs:
Another excellent specphot standard star catalog we recommend downloading is:
- Stritzinger et al., 2005, Carnegie specphot standards, availaible here
Planned future catalogs of spectrophotometric standard stars which will soon be available are:
- All-Sky HST spectrophotometric standards (Bessell et al., in prep.)
- Gaia spectrophotometric standard star catalog (Pancino et al., 2012)