Cosmology

Redshift vs. Time:

$${\frac{dz}{dt}}$$ = - H₀(1 + z)²($$\Omega_{0}^{}$$z + 1)^1/2

where z is the redshift, t the cosmic time, H₀ is Hubble's constant, and $\Omega_{0}^{}$ the current density of the universe, in units of

$${\frac{3 H_0^2}{8 \pi G}}$$

Angular Size:

$$\Delta$$$$\theta$$ = $${\frac{d(1+z)}{D}}$$

where $\Delta$$\theta$ is the angle subtended on Earth by an object of proper length d at redshift z. D is given by the expression

D = $${\frac{2c}{H_0\Omega_0^2(1+z)}}$$$$\left\{\vphantom{ \Omega_0 z + \left( \Omega_0 - 2 \right) \left[ \left( \Omega_0 z + 1\right)^{1/2} - 1 \right] }\right.$$$$\Omega_{0}^{}$$z + $$\left(\vphantom{ \Omega_0 - 2 }\right.$$$$\Omega_{0}^{}$$ - 2$$\left.\vphantom{ \Omega_0 - 2 }\right)$$$$\left[\vphantom{ \left( \Omega_0 z + 1\right)^{1/2} - 1 }\right.$$$$\left(\vphantom{ \Omega_0 z + 1}\right.$$$$\Omega_{0}^{}$$z + 1$$\left.\vphantom{ \Omega_0 z + 1}\right)^{1/2}_{}$$ - 1$$\left.\vphantom{ \left( \Omega_0 z + 1\right)^{1/2} - 1 }\right]$$ $$\left.\vphantom{ \Omega_0 z + \left( \Omega_0 - 2 \right) \left[ \left( \Omega_0 z + 1\right)^{1/2} - 1 \right] }\right\}$$

Flux:

S = $${\frac{L}{4 \pi D^2 (1+z)^2}}$$

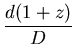
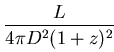
where S is the energy received per second per square metre on earth, and L is the luminosity emitted by the object at redshift z in a second (object frame).